Bouncing Barney

by

Susan Sexton

Barney is traveling inside a triangular region. He starts at a point on the perimeter of the triangle and moves along a path that is parallel to one side of the triangle until he arrives at the perimeter. Then he turns and goes down another path parallel to the side of the triangle until he arrives at the perimeter again. He goes on in this fashion.

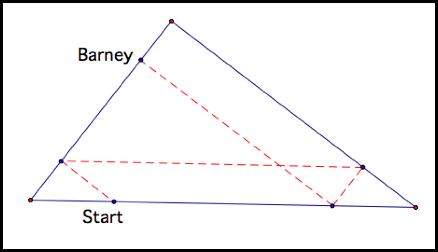
If Barney keeps going, where will he end up?

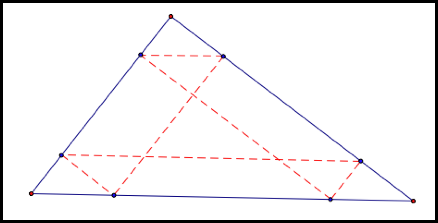
It appears that Barney arrives back at his starting point!

Here is a GSP Sketch to move Barney around.

But how long is his path?

Barney’s path is creating parallelograms.

There are some nice properties of parallelograms . . .

one being that their opposite sides are congruent.

This will help us to find out how far Barney travels.

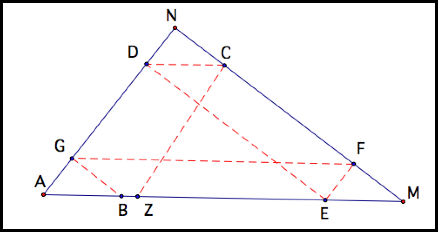
Here is a labeled figure to help us:

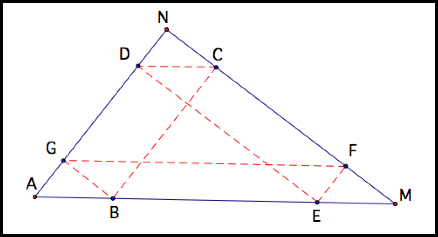
ABCD is a parallelogram so CB = DA

AEFG is a parallelogram so AE = GF

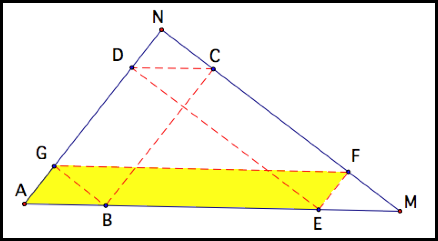
DCME is a parallelogram so DC = EM and DE = CM

NDEF is a parallelogram so ND = EF

NCBG is a parallelogram so NC = BG

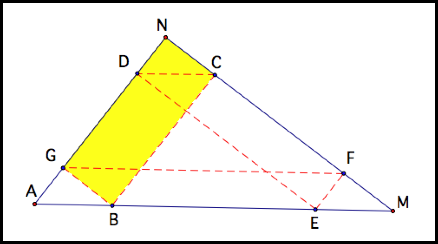
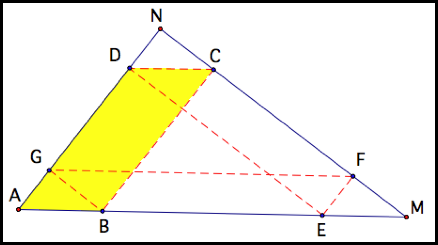
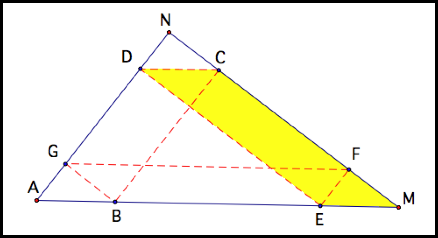
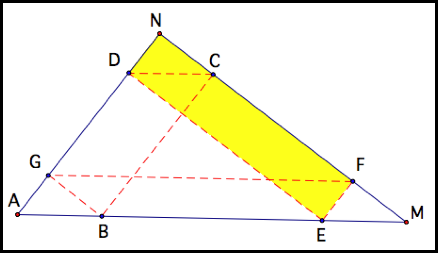
By coloring the portion of Barney’s path with its corresponding part of the perimeter of the triangle, we can see that the entire perimeter of the triangle is colored. So Barney travels the length of the triangle’s perimeter.

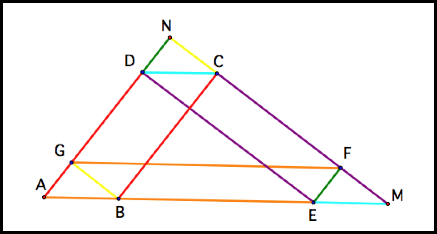
The perimeter of the triangle consists of:

AE + EM + MC + CN + ND + DA

Barney’s path is:

BG + GF + FE + ED + DC + CB

So they are equal.

So how many times does Barney hit the perimeter of the triangle before he returns to his starting point?

In the figure above he does it 5 times.

Let’s move Barney around. How about moving him closer to the midpoint of AM?

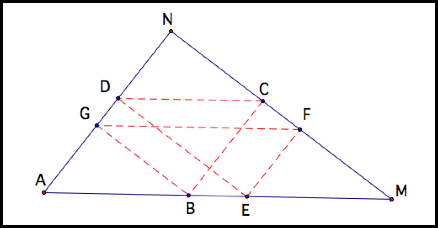
He still hits the perimeter 5 times.

What if Barney is at the midpoint of AM?

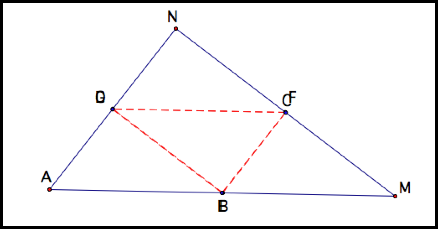
He only hits it 2 times before returning.

What if Barney goes past the midpoint?

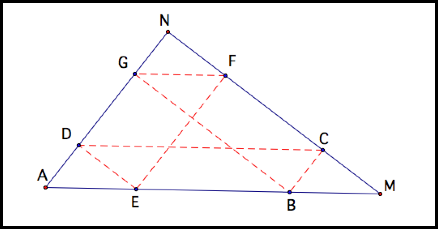
It looks like a reflection of the first diagram.

So it appears that Barney will hit the perimeter at most 5 times before he returns to the starting point.

Why does Barney return to the starting point?

Here’s a proof to show why:

First, let’s assume that Barney doesn’t return to his starting point, instead he returns to point Z.

Z will either be to the right or left of B.

Since Barney is not going to go outside the triangle he will definitely return such that A is not between Z and B.

BGFM is a parallelogram so

BG = FM, angle GBA = angle FME, and angle GAB = angle FEM

So triangle GBA is congruent to triangle FME by AAS.

Therefore AB = EM.

MEDC is a parallelogram so EM = DC.

Therefore AB = DC.

ADCZ is a parallelogram so DC = AZ.

(remember Barney only travels on parallel paths)

Therefore AB = AZ.

If A is not between B and Z (which it can’t be otherwise Barney would be outside the triangle) then B = Z.

Therefore Barney must arrive back at the same point!

What if Barney were traveling on a point outside the triangle but still on paths that are parallel to the perimeter of the triangle?

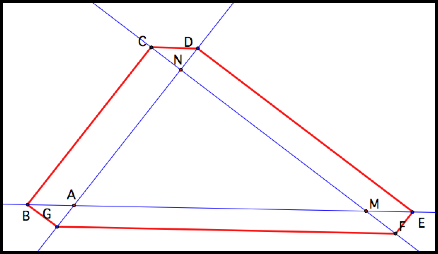
If Barney starts at point B (or any point really) then he does arrive right back to his starting point!

Return to Main Menu